Por fin se resuelve el enigma de la forma del cristal
El método puede predecir formas de cristales que carecen de simetría
La forma de un cristal viene determinada por su química inherente, una característica que en última instancia determina su forma final a partir de los detalles más básicos. Pero a veces la falta de simetría de un cristal hace que las energías superficiales de sus facetas sean desconocidas, confundiendo cualquier predicción teórica de su forma.
Imagen simbólica
Computer-generated image
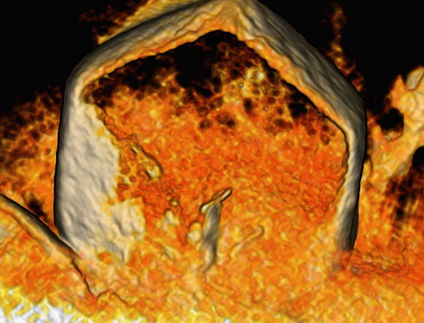
Investigadores de la Universidad de Rice han desarrollado un método para predecir cómo toman forma los cristales a partir de su química interna, incluso cuando el cristal carece de simetría. Esta representación de un cristal de nitrato de plata tiene ocho aristas, ninguna de las cuales coincide con las demás. Aun así, el algoritmo del equipo de Rice fue capaz de predecir su forma.
Illustration by Luqing Wang/Rice University
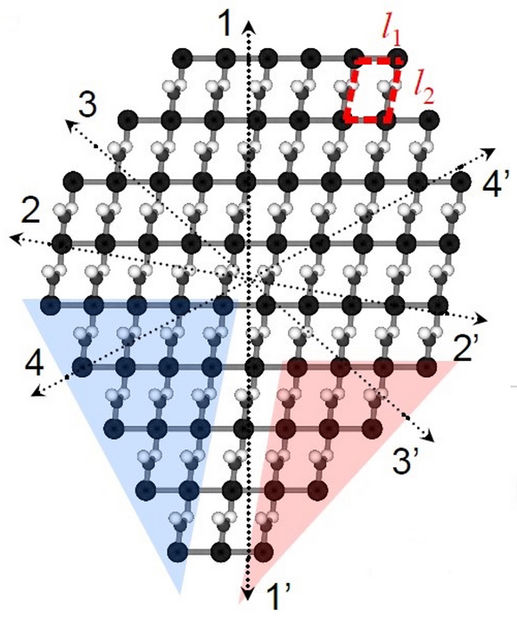
Los teóricos de la Universidad de Rice dicen haber encontrado una forma de evitar este enigma asignando energías latentes arbitrarias a sus superficies o, en el caso de los materiales bidimensionales, a sus bordes.
Sí, parece una trampa, pero del mismo modo que un mago encuentra una carta selecta en una baraja reduciendo las posibilidades, un poco de prestidigitación algebraica sirve para resolver el problema de predecir la forma de un cristal.
El método descrito en Nature Computational Science muestra que el uso de lo que llaman energías de borde auxiliares puede hacer que las predicciones vuelvan a coincidir con la construcción de Wulff, una receta geométrica que se utiliza desde hace más de un siglo para determinar cómo llegan los cristales a sus formas finales de equilibrio.
El artículo de libre acceso del físico de materiales Boris Yakobson, el autor principal y ex alumno Luqing Wang y sus colegas de la Escuela de Ingeniería George R. Brown de Rice introduce algoritmos que emplean números arbitrarios para los factores de la mano derecha en las ecuaciones y siguen ofreciendo la solución de forma única adecuada.
"El tema de la forma es convincente, pero los investigadores llevan años intentando calcular las energías superficiales de los cristales asimétricos, sin conseguirlo", explica Yakobson. "Resulta que estábamos cayendo en una madriguera de conejo, pero sabíamos que si la naturaleza puede encontrar una solución a través de un gaznate de movimientos atómicos, también debería haber una forma de determinarla para nosotros".
Dijo que el aumento del interés por los materiales 2D en los últimos tiempos motivó el nuevo estudio. "Tuvimos un momento 'eureka': Tras cambiar nuestro pensamiento geométrico por el algebraico, añadimos ecuaciones de cierre que contienen parámetros arbitrarios", dijo Yakobson. "Parecen inútiles, pero lo pasamos todo por el ordenador y observamos que salía una forma bien definida", dijo.
"Lo difícil fue convencer a nuestros revisores de que la energía de los bordes es realmente indefinible, pero aún así se puede lograr una solución", dijo Wang.
El trabajo podría proporcionar una valiosa herramienta a los investigadores que cultivan cristales de abajo arriba para aplicaciones catalíticas, emisoras de luz, sensoras, magnéticas y plasmónicas, especialmente cuando sus formas y bordes activos son de especial importancia.
Los investigadores señalaron que los cristales naturales gozan del lujo del tiempo geológico. Llegan a sus formas "realizando incesantemente un experimento de ensayo y error" mientras buscan el equilibrio, la energía mínima de todos sus átomos constituyentes.
Pero los enfoques computacionales y teóricos simplemente no pueden tratar con miles de millones de átomos a la vez, por lo que generalmente se apoyan en las energías de los átomos orientados hacia el exterior. Para muchos cristales que tienen facetas o bordes equivalentes, esto funciona bien.
En los materiales 2D, básicamente todos los átomos están "orientados hacia el exterior". Cuando sus aristas son equivalentes por simetría -en los rectángulos, por ejemplo-, completar una construcción de Wulff es sencillo tras calcular las energías de las aristas mediante la teoría del funcional de la densidad.
Pero en ausencia de simetría, cuando todas las aristas son diferentes, la energía media calculada carece de sentido, dijo Yakobson.
"La naturaleza tiene la respuesta para dar forma a un cristal independientemente de lo que 'sepa' o no sobre las energías de los bordes", dijo. "Así que hay una respuesta. Nuestro reto era imitarla con la teoría".
El primer paso hacia la solución fue renunciar conscientemente a encontrar las energías absolutas de los bordes, que no se conocen, y ocuparse en cambio de sus combinaciones computables bien definidas, dijo Yakobson. Desde el punto de vista geométrico, esto era todo un enigma y, en el caso de los materiales asimétricos a granel, resultaba irremediablemente complicado.
"Pero los materiales en 2D y sus polígonos planos facilitaban la resolución del problema en lugar de tener que lidiar con poliedros multifacéticos", dijo.
Encontrar y establecer las energías medias era sólo el primer paso, seguido de "ecuaciones de cierre" que utilizaban la energía latente arbitraria del material para el lado derecho de la ecuación. Aunque estos últimos números fueran intencionadamente incorrectos, al aplicarlos todos a la construcción de Wulff del libro de texto se obtenía la forma de cristal correcta.
El grupo probó su teoría en varios cristales 2D y comparó los resultados con las formas finales observadas de los cristales. Sus versátiles ecuaciones predijeron con éxito las formas, mostradas experimentalmente, del rectángulo truncado formado por el seleniuro de estaño 2D, un prometedor material termo y piezoeléctrico, y las agujas asimétricas formadas por el nitrito de plata.
Nota: Este artículo ha sido traducido utilizando un sistema informático sin intervención humana. LUMITOS ofrece estas traducciones automáticas para presentar una gama más amplia de noticias de actualidad. Como este artículo ha sido traducido con traducción automática, es posible que contenga errores de vocabulario, sintaxis o gramática. El artículo original en Inglés se puede encontrar aquí.
Publicación original
Más noticias del departamento ciencias
Reciba la química en su bandeja de entrada
No se pierda nada a partir de ahora: Nuestro boletín electrónico de química, análisis, laboratorio y tecnología de procesos le pone al día todos los martes y jueves. Las últimas noticias del sector, los productos más destacados y las innovaciones, de forma compacta y fácil de entender en su bandeja de entrada. Investigado por nosotros para que usted no tenga que hacerlo.
